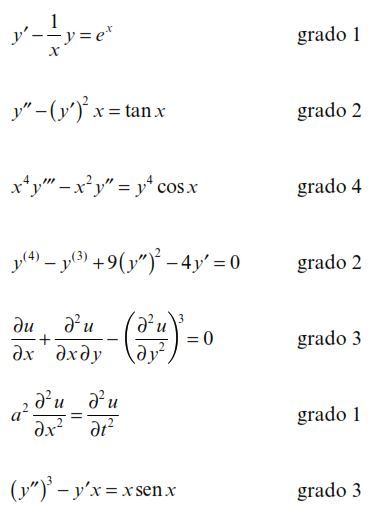Las Ecuaciones Diferenciales (ED) juegan un papel fundamental tanto en la propia Matemática como en otras ciencias como la Física, Química, Economía, etc. A diferencia de las ecuaciones algebraicas, en una ecuación diferencial la incógnita es una función (en ocasiones del tiempo), no un número. Una ecuación diferencial es una ecuación que contiene la derivada o las derivadas de una o más variables dependientes respecto de una o más variables independientes.
Los términos diferencial y ecuación indican, sin lugar a dudas, la resolución de cierto tipo de ecuaciones que contienen derivadas; sin embargo, antes de iniciar la resolución de cualquier ecuación, primero debemos aprender las definiciones elementales y la terminología del tema.
Definición: La derivada \(\frac{dy}{dx}\) de una función \(y = \phi(x)\) representa en sí misma otra función \(\phi'(x)\) que se encuentra mediante una regla específica. Por ejemplo, la función \(y = e^{0.1x^{2}}\) es diferenciable sobre el intervalo \((-\infty, \infty)\), y su derivada es \(\frac{dy}{dx} = 0.2xe^{0.1x^{2}}\) .
Si reemplazamos \(e^{0.1x^{2}}\) por el símbolo \(y\), obtenemos:
$$\frac{dy}{dx}= 0.2xy$$ (1)
Ahora imagine que un amigo suyo le proporciona solo la ecuación diferencial de la expresión (1), y que usted no tiene idea de cómo se obtuvo. Su amigo le pregunta: ¿Cuál es la función representada por el símbolo y? Entonces, usted se enfrenta a uno de los problemas básicos encontrados en un curso de ecuaciones diferenciales: ¿Cómo resolver una ecuación de este tipo para la función incógnita \(y = \phi(x)\)? Tal cuestión es más o menos equivalente al conocido problema del inverso del cálculo diferencial: dada una derivada, encontrar una antiderivada.
Definición de Ecuación Diferencial
Se dice que una ecuación diferencial (ED) es cualquier ecuación que contiene las derivadas de una o más variables dependientes con respecto a una o más variables independientes. En un curso de álgebra elemental se aprende que para resolver la ecuación \(ax + b = 0\) hay que realizar un “despeje” de la variable \(x\), porque se trata de una ecuación lineal en una variable. Si la ecuación por resolver es de la forma \(ax^2 + bx + c = 0\), sabemos que por tratarse de una ecuación cuadrática, la fórmula general es una opción. La clasificación de las ecuaciones permite elegir el método de solución adecuado.
Con las ecuaciones diferenciales sucede lo mismo: dada una ecuación diferencial, es primordial identificar su forma para que a partir de esto se elija correctamente el procedimiento de solución. De esta manera, es necesario caracterizar las ecuaciones diferenciales. Con el objetivo de referirnos a ellas, debemos clasificar las ecuaciones diferenciales por tipo, orden y linealidad.
Clasificación por tipo
De acuerdo con su tipo, las ecuaciones diferenciales pueden clasificarse en ordinarias y parciales. Si una ecuación diferencial contiene únicamente derivadas ordinarias de una o más variables dependientes con respecto a una sola variable independiente, se dice que es una ecuación diferencial ordinaria (EDO). Por ejemplo:
$$\frac{dy}{dx}+ 5y = e^x , \frac{{d^2}y}{dx^2} – \frac{dy}{dx} + 6y = 0 , \frac{dx}{dt} + \frac{dy}{dt} = 2x + y $$ (2)
Una ecuación en la que se presentan las derivadas parciales de una o más variables dependientes de dos o más variables independientes se denomina Ecuación Diferencial Parcial (EDP). Por ejemplo:
$$\frac{{\partial^2}u}{\partial{x^2}}+ \frac{{\partial^2}u}{\partial{y^2}} = 0 , \frac{{\partial^2}u}{\partial{x^2}} = \frac{{\partial^2}u}{\partial{t^2}} – 2\frac{\partial{u}}{\partial{t}} , \frac{\partial{u}}{\partial{y}} = – \frac{\partial{v}}{\partial{x}}$$ (3)
De esta forma, por su tipo, las ecuaciones diferenciales son ordinarias (si solo existe una única variable independiente) o parciales (si existen dos o más variables independientes).
Notación
las derivadas ordinarias se representan utilizando la notación de Leibniz \(\frac{dy}{dx}\), \(\frac{d^2y}{dx^2}\), \(\frac{d^3y}{dx^3}\), … , o la notación prima \( y\prime , y\prime\prime , y\prime\prime\prime , … \) Si se emplea esta última notación, las primeras dos ecuaciones diferenciales mostradas en (2) pueden expresarse de forma más compacta como \(y^\prime + 5y = e^x\) y \(y\prime\prime – y\prime + 6y = 0\). En realidad, la notación de prima se utiliza para señalar solamente las primeras tres derivadas; la cuarta derivada se indica como \(y^{(4)}\) en lugar de \( y\prime\prime\prime\prime\). En términos generales, la n-ésima derivada n será \({d^ny}/{dx^n}\) o \(y^{(n)}\).
A pesar de ser menos conveniente de escribir y formar tipográficamente, la notación de Leibniz presenta una ventaja sobre la notación de prima en el sentido de que indica con claridad las variables independientes y dependientes. Por ejemplo, en la ecuación diferencial \(\frac{d^2x}{dt^2} + 16 = 0\), se observa de forma inmediata que el símbolo x representa ahora a la variable dependiente, mientras que la variable independiente será t.
Clasificación por orden
El orden es otra manera de clasificar las ecuaciones diferenciales (EDO o EDP), se representa por el orden de la derivada más alta que aparece en la ecuación. Por ejemplo.

Clasificación por linealidad
En un curso de álgebra lineal se aprende que una ecuación lineal en dos variables es una expresión de la forma \(ax + by = c\). La característica principal de esta ecuación es que las variables están elevadas a la potencia 1. De la misma manera, una ecuación diferencial lineal tiene como propiedad que la variable dependiente y todas sus derivadas están elevadas a la potencia 1. Así, una ecuación diferencial ordinaria se denomina lineal si es de la forma:
$${a_n}(x){y^{(n)}} + a_{n-1}(x)y^{(n-1)} + … + a_2(x)y\prime\prime + a_1(x)y/prime + a_0(x)y = g(x)$$
Si \(g(x) = 0\) la ecuación se denomina homogénea. Si \(g(x) ≠ 0\), la ecuación es no homogénea. Si una ecuación no tiene la forma anterior, entonces se dice que la ecuación es No Lineal.
Una ecuación diferencial lineal es ordinaria si la variable dependiente, así como cualquiera de sus derivadas, aparecen elevadas a la potencia 1. De igual forma, la función \(g(x)\) y cada una de las funciones que aparecen como coeficientes de las derivadas son funciones que dependen todas de la misma variable independiente considerada en la ecuación.
Grado de una Ecuación Diferencial
Para determinar el orden de una ecuación diferencial consideramos la derivada más alta de la ecuación, sin importar el exponente al que estén elevadas las derivadas y la variable dependiente. Tal exponente se conoce como el grado de la ecuación diferencial.
Así, si consideramos el exponente más grande a la cual está elevada una variable dependiente, o bien alguna de sus derivadas, se conoce como grado de una ecuación diferencial, las siguientes ecuaciones tienen los grados indicados: